With due apology to all the Masters who gave the koan to humanity to spur them into thinking of higher realities and higher dimensions, I will try to model a Zen koan into a probabilistic framework, as my own exploration and answer to it.
This is the said famous koan: “In a remote forest, if a bamboo tree falls by itself, unseen, unheard by anyone, does the bamboo tree make a sound?”
The answer to this question lies in differentiating between the fall of tree being observed and not being observed by a being. Since a fall will always produce a sound, due to matter coming in contact with other matter particles, we assume that if the tree falls, it will make a sound.
Since the bamboo tree falls by itself, we will assume that no other object or event contributes to making the sound other than its fall.
This can be seen as a problem in conditional probability, where we determine the probability of hearing a sound, subject to the condition of observing the tree falling.
When the tree is observed by a human being with a conscious will, the person has the power to lessen the chances, or even stop the tree from falling. Ofcourse, a destructive person can accelerate the fall, or even chop off the tree hi/herself for their own selfish reasons, but for the sake of this problem, we will assume that the person uses his/her will to reduce the likelihood of the fall of the tree.
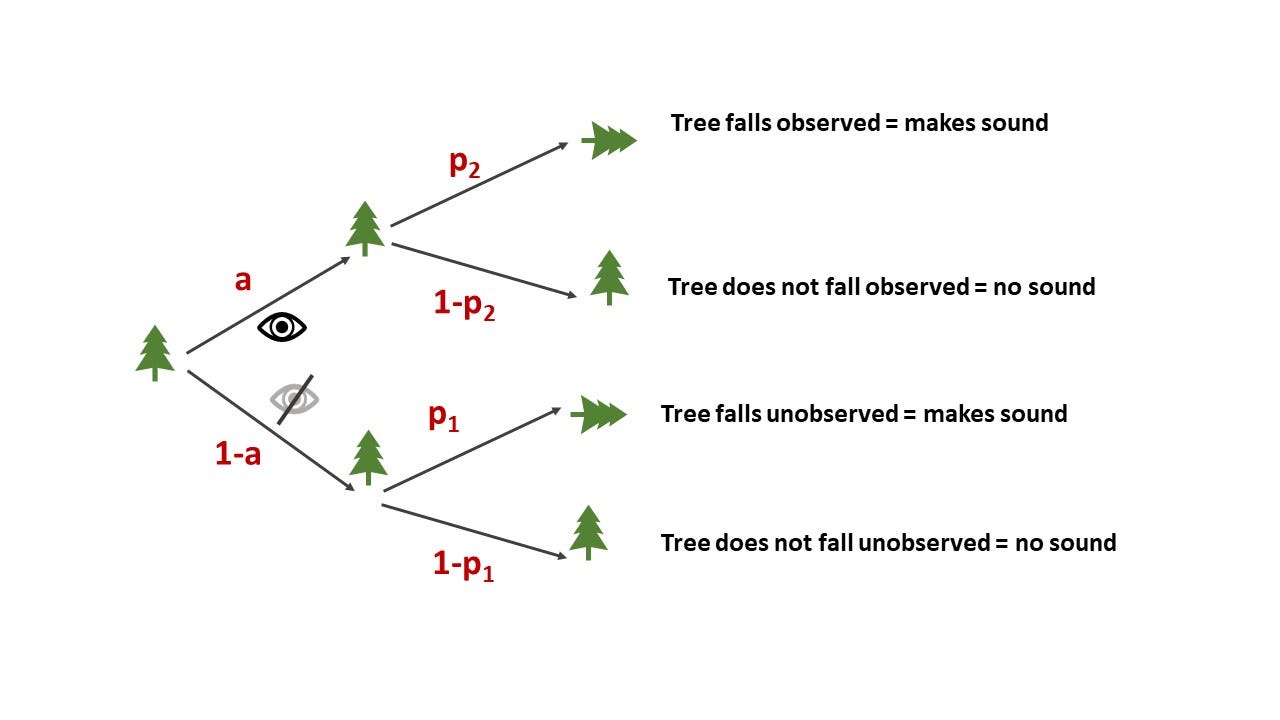
Let the probability that a conscious human being A is available to observe the tree = a
Let the probability of the tree falling, when unobserved = p1
Let the probability of the tree falling, when observed by said person A = p2
p2 < p1 by assumption
So we can write the different conditional probabilities as follows:
P (Tree falls) = P (Fall | Observed) x P (obs) + P (Fall | Unobserved) x P (unobs)
= a.p2 + (1 – a)p1 = 1 – a(p1 – p2)
P (Tree does not fall) = P (No fall | Observed) x P (obs) + P (No fall | Unobserved) x P (unobs)
= (1 – p2).a + (1 – p1)(1 – a)
= 2 + a(p1 – p2) – p1
Normalizing the probabilities gives:
Probability of tree falling = [1 – a(p1 – p2)] / (3 – p1)
Probability of tree not falling = [2 + a(p1 – p2) – p1] / (3 – p1)
In this, if we consider p1 = p2, the term that contains a cancels out in the sum of the two probabilities, and the total probability is 1, so this expression is correct. It basically means, that if the probability of the tree falling is the same when the tree is observed or not observed, then the presence of the person does not matter. The tree falls with a probability p = p1, and makes sound with the same probability. Which is how it should be, from our initial assumption.
The most remarkable thing about this problem is that we can never ascertain what isp1. To ascertain p1, we would have to observe lots of trees falling, and estimate the probability. But the moment we observe the tree, it is no longer p1! It is now p2.
Now, if we plug in p2=0, then the probability of the tree falling = (1-a).p1
Which means, that if a person observing the tree can stop the tree from falling, then (1-a).p1 is the probability that the tree will fall and a sound will be heard.
Now, if no one is available to observe the tree to fall, and we know this to be the case, then the probability of the tree falling = (1-a).p1 = p1 (a = 0)
Since a & p1 are both fractions, (1-a).p1 < p1
It means that even if there is a non zero probability of someone observing the tree & stopping it from falling, the probability of the tree falling reduces.
As is evident from the model, as p2 decreases, the probability of tree falling decreases, all else being equal. And we know that p1 can not be determined.
If we know that an observer is present (a =1), and if the observer has the power to reduce probability of tree falling to zero (p2 = 0), the probability of tree falling becomes zero. That is the only scenario in which probability of tree falling can be zero (Since we can never determine if p1 is non zero or not).
The purpose of this analysis is to answer this age-old question in an objective manner, which helps weigh different aspects of the problem without getting muddled with too many variables at one time. It answers the questions one at a time.